2022年，公司刘岩副教授团队在计算科学和工程领域国际著名期刊《Computer Methods in Applied Mechanics and Engineering》（SCI TOP期刊）发表了题为“A geometrically exact discrete elastic rod model based on improved discrete curvature”的研究论文（论文链接：https://doi.org/10.1016/j.cma.2022.114640），公司为第一完成单位，刘岩副教授为通讯作者。

该文提出一种基于改进离散曲率的离散几何精确弹性杆模型。该模型是离散微分几何中基尔霍夫-洛夫杆有限差分类型离散化的扩展，具有4个未知数，包括轴的平移位移和轴向横截面旋转。杆轴线和横截面的正交性通过伪时间的平行传输来保证。新定义的统一离散曲率提出了5种加权函数方案，其中三个是通过减少旋转矢量的泰勒展开的最大非线性项提出的，理论和数值试验表明，与传统方法相比，这三种方法可以提高模型的精度。方案5在推荐方案中表现最佳。在离散微分几何模型中引入了平移和端部旋转的自由变换，通过这种技术可以方便自然地实现杆段、旋转边界和外部端部力矩之间的刚性连接，还通过几个合适的数值实例验证和研究了收敛性、客观性和对细长比的不敏感性等重要特性。此外，结果表明，与连续梁相比，使用离散曲率使具有柔性连接的刚性杆系统具有更好的性能。

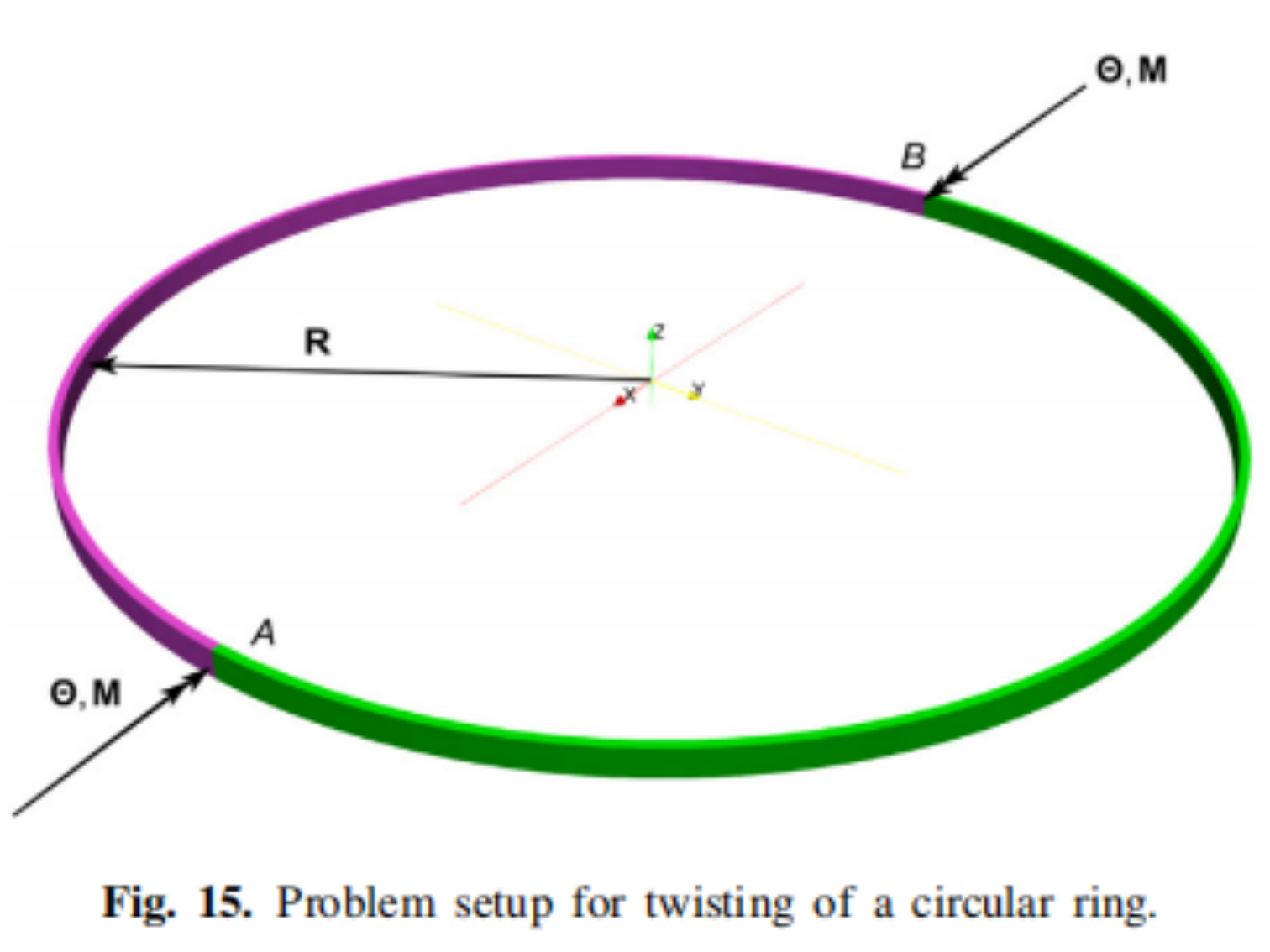
图1 圆环扭曲的问题设置

图2 反应力矩-旋转曲线